In this paper we consider the nonlinear viscoelastic equation
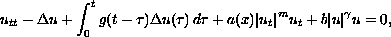
in a bounded domain. Without imposing geometry restrictions on the boundary, we establish an exponential decay result, under weaker conditions than those in [3].
Said Berrimi, Salim A. Messaoudi
Abstract:
In this paper we consider the nonlinear viscoelastic equation
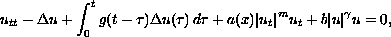
in a bounded domain. Without imposing geometry restrictions
on the boundary, we establish an exponential decay result,
under weaker conditions than those in [3].
Submitted May 17, 2004. Published June 29, 2004.
Math Subject Classifications: 35B35, 35L20, 35L70.
Key Words: Exponential decay; global existence; nonlinear localized damping.
Show me the PDF file (219K), TEX file, and other files for this article.
 |
Said Berrimi Math Department University of Setif Setif, Algeria email: berrimi@yahoo.fr |
|---|---|
 |
Salim A. Messaoudi Mathematical Sciences Department KFUPM, Dhahran 31261, Saudi Arabia email: messaoud@kfupm.edu.sa |
Return to the EJDE web page