Electron. J. Diff. Eqns.,
Vol. 2004(2004), No. 77, pp. 1-7.
Blow-up of solutions to a nonlinear wave equation
Svetlin G. Georgiev
Abstract:
We study the solutions to the the radial 2-dimensional wave equation
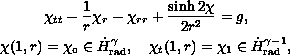
where
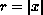 and
and
 in
in
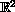 .
We show that this Cauchy problem, with values into a
hyperbolic space, is ill posed in subcritical Sobolev spaces.
In particular, we construct a function
.
We show that this Cauchy problem, with values into a
hyperbolic space, is ill posed in subcritical Sobolev spaces.
In particular, we construct a function
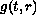 in the space
in the space
![$L^p([0,1]L_{\rm rad}^q)$](gifs/af.gif) ,
with
,
with
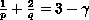 ,
,
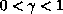 ,
,
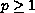 , and
, and
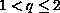 , for which the solution satisfies
, for which the solution satisfies
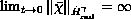 .
In doing so, we provide a counterexample to estimates
in [1].
.
In doing so, we provide a counterexample to estimates
in [1].
Submitted March 16, 2004. Published May 26, 2004.
Math Subject Classifications: 35L10, 35L50
Key Words: Wave equation, blow-up, hyperbolic space.
Show me the
PDF file (205K),
TEX file, and other files for this article.
 |
Svetlin Georgiev Georgiev
University of Sofia
Faculty of Mathematics and Informatics
Department of Differential Equations, Bulgaria
email: sgg2000bg@yahoo.com |
|---|
Return to the EJDE web page
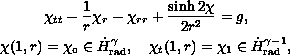
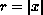 and
and
 in
in
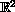 .
We show that this Cauchy problem, with values into a
hyperbolic space, is ill posed in subcritical Sobolev spaces.
In particular, we construct a function
.
We show that this Cauchy problem, with values into a
hyperbolic space, is ill posed in subcritical Sobolev spaces.
In particular, we construct a function
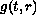 in the space
in the space
![$L^p([0,1]L_{\rm rad}^q)$](gifs/af.gif) ,
with
,
with
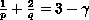 ,
,
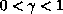 ,
,
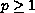 , and
, and
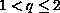 , for which the solution satisfies
, for which the solution satisfies
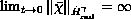 .
In doing so, we provide a counterexample to estimates
in [1].
.
In doing so, we provide a counterexample to estimates
in [1].
