Electron. J. Diff. Eqns., Vol. 2004(2004), No. 72, pp. 1-25.
Exact multiplicity results for a p-Laplacian positone
problem with concave-convex-concave nonlinearities
Idris Addou & Shin-Hwa Wang
Abstract:
We study the exact number of positive solutions of a two-point Dirichlet
boundary-value problem involving the p-Laplacian operator.
We consider the case
 and the case
and the case
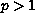 , when the
nonlinearity satisfies
, when the
nonlinearity satisfies
 (positone) and has three distinct
simple positive zeros and such that
(positone) and has three distinct
simple positive zeros and such that
 changes sign exactly twice on
changes sign exactly twice on
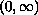 .
Note that we may allow
.
Note that we may allow
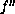 to
change sign more than twice on
to
change sign more than twice on
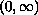 .
We also present
some interesting examples.
.
We also present
some interesting examples.
Submitted March 8, 2004. Published May 20, 2004.
Math Subject Classifications: 34B18, 34B15.
Key Words: Exact multiplicity result, p-Laplacian, positone problem,
bifurcation, concave-convex-concave nonlinearity,
positive solution, dead core solution, time map.
Show me the
PDF file (1398K),
TEX file, and other files for this article.
 |
Idris Addou
Departement de Mathematiques et Statistiques
Universite de Montreal
C.P. 6128, Succ. Centre-ville, Montreal, Quebec, Canada, H3C2J7
email: addou@dms.umontreal.ca |
 |
Shin-Hwa Wang
Department of Mathematics
National Tsing Hua University
Hsinchu, Taiwan 300, Republic of China
email: shwang@math.nthu.edu.tw |
|---|
Return to the EJDE web page
 and the case
and the case
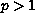 , when the
nonlinearity satisfies
, when the
nonlinearity satisfies
 (positone) and has three distinct
simple positive zeros and such that
(positone) and has three distinct
simple positive zeros and such that
 changes sign exactly twice on
changes sign exactly twice on
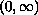 .
Note that we may allow
.
Note that we may allow
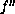 to
change sign more than twice on
to
change sign more than twice on
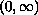 .
We also present
some interesting examples.
.
We also present
some interesting examples.

