Electron. J. Diff. Eqns., Vol. 2004(2004), No. 65, pp. 1-8.
Finite order solutions of complex linear differential equations
Ilpo Laine & Ronghua Yang
Abstract:
We shall consider the growth of solutions of complex linear
homogeneous differential equations
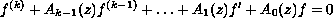
with entire coefficients. If one of the intermediate coefficients
in exponentially dominating in a sector and
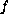 is of finite
order, then a derivative
is of finite
order, then a derivative
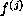 is asymptotically constant in a
slightly smaller sector. We also find conditions on the
coefficients to ensure that all transcendental solutions are of
infinite order. This paper extends previous results due to
Gundersen and to Belaidi and Hamani.
is asymptotically constant in a
slightly smaller sector. We also find conditions on the
coefficients to ensure that all transcendental solutions are of
infinite order. This paper extends previous results due to
Gundersen and to Belaidi and Hamani.
Submitted December 10, 2003. Published April 28, 2004.
Math Subject Classifications: 30D35, 34M10.
Key Words: Linear differential equations, growth of solutions, iterated order.
Show me the
PDF file (215K),
TEX file, and other files for this article.
 |
Ilpo Laine
University of Joensuu, Department of Mathematics
P. O. Box 111, FIN-80101 Joensuu, Finland
email: ilpo.laine@joensuu.fi |
|---|
 |
Ronghua Yang
University of Joensuu, Department of Mathematics
P. O. Box 111, FIN-80101 Joensuu, Finland
email: ronghua.yang@joensuu.fi |
|---|
Return to the EJDE web page
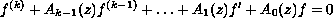
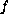 is of finite
order, then a derivative
is of finite
order, then a derivative
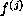 is asymptotically constant in a
slightly smaller sector. We also find conditions on the
coefficients to ensure that all transcendental solutions are of
infinite order. This paper extends previous results due to
Gundersen and to Belaidi and Hamani.
is asymptotically constant in a
slightly smaller sector. We also find conditions on the
coefficients to ensure that all transcendental solutions are of
infinite order. This paper extends previous results due to
Gundersen and to Belaidi and Hamani.

