Electron. J. Diff. Eqns., Vol. 2004(2004), No. 61, pp. 1-15.
Asymptotically almost periodic and almost periodic solutions
for a class of evolution equations
Eduardo Hernandez M, Mauricio L. Pelicer, & Jose P. C. dos Santos
Abstract:
In this paper we study the existence of asymptotically almost periodic
and almost periodic solutions for the partial evolution equation
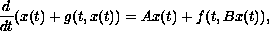
where
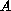 is the infinitesimal generator of an analytic semigroup on a
Banach space
is the infinitesimal generator of an analytic semigroup on a
Banach space
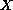 ,
,
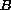 is a closed linear operator, and
is a closed linear operator, and
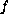 ,
,
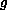 are
given functions.
are
given functions.
Submitted February 20, 2004. Published April 21, 2004.
Math Subject Classifications: 34K14, 34K30.
Key Words: Almost periodic, asymptotically almost periodic,
semigroup of linear operators.
Show me the
PDF file (281K),
TEX file, and other files for this article.
 |
Eduardo Hernandez M.
Departamento de Matematica
Instituto de Ciencias Matematicas de Sao Carlos
Universidade de Sao Paulo,
Caixa Postal 668
13560-970 Sao Carlos, SP. Brazil
email: lalohm@icmc.sc.usp.br |
|---|
 |
Mauricio L. Pelicer
Departamento de Matematica
Instituto de Ciencias Matematicas de Sao Carlos
Universidade de Sao Paulo,
Caixa Postal 668
13560-970 Sao Carlos, SP. Brazil
email: mpelicer@icmc.sc.usp.br |
|---|
 |
Jose P. C. dos Santos
Departamento de Matematica
Instituto de Ciencias Matematicas de Sao Carlos
Universidade de Sao Paulo,
Caixa Postal 668
13560-970 Sao Carlos, SP. Brazil
email: zepaulo@icmc.sc.usp.br |
|---|
Return to the EJDE web page
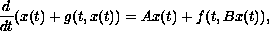
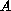 is the infinitesimal generator of an analytic semigroup on a
Banach space
is the infinitesimal generator of an analytic semigroup on a
Banach space
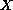 ,
,
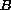 is a closed linear operator, and
is a closed linear operator, and
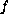 ,
,
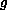 are
given functions.
are
given functions.


