Electron. J. Diff. Eqns., Vol. 2004(2004), No. 55, pp. 1-19.
Homogenization and uniform stabilization for a nonlinear
hyperbolic equation in domains with holes of small capacity
Marcelo M. Cavalcanti, Valeria N. Domingos Cavalcanti,
Juan A. Soriano, Joel S. Souza
Abstract:
In this article we study the homogenization and
uniform decay of the nonlinear hyperbolic equation
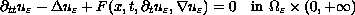
where
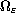 is a domain containing holes with
small capacity (i. e. the holes are smaller than a critical size).
The homogenization's proofs are based on the abstract framework
introduced by Cioranescu and Murat [8] for the study of
homogenization of elliptic problems. Moreover, uniform decay
rates are obtained by considering the perturbed energy method
developed by Haraux and Zuazua [10].
is a domain containing holes with
small capacity (i. e. the holes are smaller than a critical size).
The homogenization's proofs are based on the abstract framework
introduced by Cioranescu and Murat [8] for the study of
homogenization of elliptic problems. Moreover, uniform decay
rates are obtained by considering the perturbed energy method
developed by Haraux and Zuazua [10].
Submitted September 23, 2003. Published April 9, 2004.
Math Subject Classifications: 35B27, 35B40, 35L05
Key Words: Homogenization, asymptotic stability, wave equation.
Show me the
PDF file (315K),
TEX file, and other files for this article.
 |
Marcelo M. Cavalcanti
Universidade Estadual de Maringa
87020-900 Maringa - PR, Brasil
email: mmcavalcanti@uem.br |
|---|
 |
Valeria N. Domingos Cavalcanti
Universidade Estadual de Maringa
87020-900 Maringa - PR, Brasil
email: vndcavalcanti@uem.br |
|---|
 |
Juan Amadeo Soraino
Universidade Estadual de Maringa
87020-900 Maringa - PR, Brasil
email: jaspalomino@uem.br |
|---|
| |
Joel S. Souza
Departamento de Matematica
Universidade Federal de Santa Catarina
80040-900 Florianopolis - SC, Brasil
email: cido@dme.ufpb.br |
|---|
Return to the EJDE web page
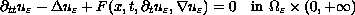
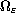 is a domain containing holes with
small capacity (i. e. the holes are smaller than a critical size).
The homogenization's proofs are based on the abstract framework
introduced by Cioranescu and Murat [8] for the study of
homogenization of elliptic problems. Moreover, uniform decay
rates are obtained by considering the perturbed energy method
developed by Haraux and Zuazua [10].
is a domain containing holes with
small capacity (i. e. the holes are smaller than a critical size).
The homogenization's proofs are based on the abstract framework
introduced by Cioranescu and Murat [8] for the study of
homogenization of elliptic problems. Moreover, uniform decay
rates are obtained by considering the perturbed energy method
developed by Haraux and Zuazua [10].


