Electron. J. Diff. Eqns., Vol. 2004(2004), No. 50, pp. 1-14.
Local invariance via comparison functions
Ovidiu Carja, Mihai Necula, & Ioan I. Vrabie
Abstract:
We consider the ordinary differential equation
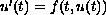 ,
where
,
where
![$f:[a,b]\times D\to \mathbb{R}^n$](gifs/ab.gif) is a given function,
while
is a given function,
while
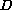 is an open subset in
is an open subset in
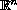 .
We prove that, if
.
We prove that, if
 is locally closed and there exists a comparison
function
is locally closed and there exists a comparison
function
![$\omega:[a,b]\times\mathbb{R}_+\to \mathbb{R}$](gifs/af.gif) such that
such that
![$$
\liminf_{h\downarrow 0}\frac{1}{h}\big[d(\xi+hf(t,\xi);K)-d(\xi;K)\big]
\leq\omega(t,d(\xi;K))
$$](gifs/ag.gif)
for each
![$(t,\xi)\in [a,b]\times D$](gifs/ah.gif) ,
then
,
then
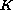 is locally invariant with respect to
is locally invariant with respect to
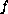 .
We show further that, under some natural extra condition,
the converse statement is also true.
.
We show further that, under some natural extra condition,
the converse statement is also true.
Submitted June 18, 2003. Published April 6, 2004.
Math Subject Classifications: 34A12, 34A34, 34C05,34C40, 34C99.
Key Words: Viable domain, local invariant subset, exterior tangency
condition, comparison property, Lipschitz retract.
Show me the
PDF file (298K),
TEX file, and other files for this article.
 |
Ovidiu Carja
Faculty of Mathematics, ``Al. I. Cuza" University
700506 Iasi, Romania
email: ocarja@uaic.ro |
|---|
 |
Mihai Necula
Faculty of Mathematics, ``Al. I. Cuza" University
700506 Iasi, Romania
email: necula@uaic.ro |
|---|
 |
Ioan I. Vrabie
Faculty of Mathematics, ``Al. I. Cuza" University
700506 Iasi, Romania
email: ivrabie@uaic.ro |
|---|
Return to the EJDE web page
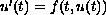 ,
where
,
where
![$f:[a,b]\times D\to \mathbb{R}^n$](gifs/ab.gif) is a given function,
while
is a given function,
while
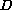 is an open subset in
is an open subset in
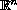 .
We prove that, if
.
We prove that, if
 is locally closed and there exists a comparison
function
is locally closed and there exists a comparison
function
![$\omega:[a,b]\times\mathbb{R}_+\to \mathbb{R}$](gifs/af.gif) such that
such that
![$$
\liminf_{h\downarrow 0}\frac{1}{h}\big[d(\xi+hf(t,\xi);K)-d(\xi;K)\big]
\leq\omega(t,d(\xi;K))
$$](gifs/ag.gif)
![$(t,\xi)\in [a,b]\times D$](gifs/ah.gif) ,
then
,
then
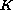 is locally invariant with respect to
is locally invariant with respect to
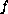 .
We show further that, under some natural extra condition,
the converse statement is also true.
.
We show further that, under some natural extra condition,
the converse statement is also true.


