We establish the existence of multiple positive solutions to the nonlinear second-order triple-point boundary-value problem on time scales,
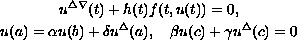
for
![$t\in[a,c]\subset\mathbb{T}$](gifs/ab.gif) , where
, where
 is a time scale,
is a time scale,
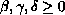 with
with
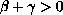 ,
,
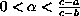 and
and
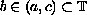 .
.
Douglas R. Anderson
Abstract:
We establish the existence of multiple positive solutions to the
nonlinear second-order triple-point boundary-value problem on
time scales,
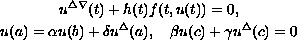
for
![$t\in[a,c]\subset\mathbb{T}$](gifs/ab.gif) , where
, where
 is a time scale,
is a time scale,
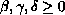 with
with
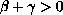 ,
,
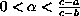 and
and
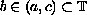 .
.
Submitted March 7, 2004. Published April 6, 2004.
Math Subject Classifications: 34B10, 34B15, 39A10.
Key Words: Fixed-point theorems, time scales, dynamic equations, cone.
Show me the PDF file (224K), TEX file, and other files for this article.
 |
Douglas R. Anderson Department of Mathematics and Computer Science Concordia College, Moorhead, Minnesota 56562, USA email: andersod@cord.edu |
|---|
Return to the EJDE web page