The main purpose of this investigation is to show that a pendulum, whose pivot oscillates vertically in a periodic fashion, has uncountably many chaotic orbits. The attribute chaotic is given according to the criterion we now describe. First, we associate to any orbit a finite or infinite sequence as follows. We write 1 or
every time the pendulum crosses the position
of unstable equilibrium with positive (counterclockwise) or negative
(clockwise) velocity, respectively. We write 0 whenever we find a
pair of consecutive zero's of the velocity separated only by a
crossing of the stable equilibrium, and with the understanding that
different pairs cannot share a common time of zero velocity.
Finally, the symbol
,
that is used only as the ending
symbol of a finite sequence, indicates that the orbit tends
asymptotically to the position of unstable equilibrium. Every
infinite sequence of the three symbols
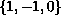represents a real
number of the interval
![$[0,1]$](gifs/ad.gif)
written in base 3 when
is replaced
with 2. An orbit is considered chaotic whenever the associated
sequence of the three symbols
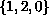is an irrational number of
.
Our main goal is to show that there are uncountably
many orbits of this type.
