In this article, we study a complete
 -order
differential equation
subject to the
-order
differential equation
subject to the
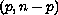 right focal boundary conditions plus an
additional nonlocal constrain. We establish sufficient conditions for
the existence of a family of positive and monotone solutions at resonance.
The emphasis in this paper is not only that the nonlinearity depends on
all higher-order derivatives but mainly that the obtaining solution
satisfies the above extra condition. Our approach is based on the
Sperner's Lemma, proposing in this way an alternative to the classical
methodologies based on fixed point or degree theory and results the
introduction of a new set of quite natural hypothesis.
right focal boundary conditions plus an
additional nonlocal constrain. We establish sufficient conditions for
the existence of a family of positive and monotone solutions at resonance.
The emphasis in this paper is not only that the nonlinearity depends on
all higher-order derivatives but mainly that the obtaining solution
satisfies the above extra condition. Our approach is based on the
Sperner's Lemma, proposing in this way an alternative to the classical
methodologies based on fixed point or degree theory and results the
introduction of a new set of quite natural hypothesis.
