Electron. J. Diff. Eqns., Vol. 2004(2004), No. 19, pp. 1-10.
Existence of solutions to nonlocal and singular elliptic
problems via Galerkin method
Francisco Julio S. A. Correa & Silvano D. B. Menezes
Abstract:
We study the existence of solutions to the nonlocal elliptic equation
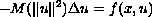
with zero Dirichlet boundary conditions on a bounded and smooth
domain of
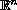 .
We consider the
.
We consider the
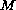 -linear case with
-linear case with
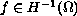 ,
and the sub-linear case
,
and the sub-linear case
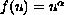 ,
,
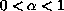 .
Our main tool is the Galerkin method for both cases when
.
Our main tool is the Galerkin method for both cases when
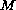 continuous and when
continuous and when
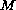 is discontinuous.
is discontinuous.
Submitted December 15, 2003. Published February 11, 2004.
Math Subject Classifications: 35J60, 35J25.
Key Words: Nonlocal elliptic problems, Galerkin Method.
Show me the
PDF file (199K),
TEX file, and other files for this article.
 |
Francisco Julio S. A. Correa
Departamento de Matematica-CCEN
Universidade Federal do Para
66.075-110 Belem Para Brazil
email: fjulio@ufpa.br |
|---|
 |
Silvano D. B. Menezes
Departamento de Matematica-CCEN
Universidade Federal do Para
66.075-110 Belem Para Brazil
email: silvano@ufpa.br |
|---|
Return to the EJDE web page
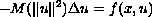
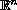 .
We consider the
.
We consider the
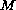 -linear case with
-linear case with
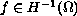 ,
and the sub-linear case
,
and the sub-linear case
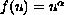 ,
,
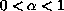 .
Our main tool is the Galerkin method for both cases when
.
Our main tool is the Galerkin method for both cases when
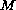 continuous and when
continuous and when
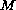 is discontinuous.
is discontinuous.

