Electron. J. Diff. Eqns., Vol. 2004(2004), No. 144, pp. 1-18.
Quasilinear elliptic systems in divergence form
with weak monotonicity and nonlinear physical data
Fabien Augsburger, Norbert Hungerbühler
Abstract:
We study the quasilinear elliptic system
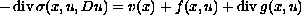
on a bounded domain of
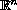 with homogeneous
Dirichlet boundary conditions.
This system corresponds to a diffusion problem with a source
with homogeneous
Dirichlet boundary conditions.
This system corresponds to a diffusion problem with a source
 in a moving and dissolving substance, where the motion is
described by
in a moving and dissolving substance, where the motion is
described by
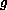 and the dissolution by
and the dissolution by
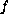 .
We prove existence of a weak solution of this system under
classical regularity, growth, and coercivity conditions for
.
We prove existence of a weak solution of this system under
classical regularity, growth, and coercivity conditions for
 ,
but with only very mild monotonicity assumptions.
,
but with only very mild monotonicity assumptions.
Submitted August 16, 2004. Published December 7, 2004.
Math Subject Classifications: 35J60.
Key Words: Young measure; noninear elliptic systems.
Show me the
PDF file (319K),
TEX file, and other files for this article.
 |
Fabien Augsburger
Department of Mathematics
University of Fribourg, Pérolles
1700 Fribourg, Switzerland
email: norbert.hungerbuehler@unifr.ch |
|---|
 |
Norbert Hungerbühler
Department of Mathematics
University of Fribourg, Pérolles
1700 Fribourg, Switzerland
email: norbert.hungerbuehler@unifr.ch |
|---|
Return to the EJDE web page
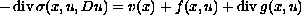
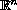 with homogeneous
Dirichlet boundary conditions.
This system corresponds to a diffusion problem with a source
with homogeneous
Dirichlet boundary conditions.
This system corresponds to a diffusion problem with a source
 in a moving and dissolving substance, where the motion is
described by
in a moving and dissolving substance, where the motion is
described by
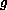 and the dissolution by
and the dissolution by
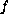 .
We prove existence of a weak solution of this system under
classical regularity, growth, and coercivity conditions for
.
We prove existence of a weak solution of this system under
classical regularity, growth, and coercivity conditions for
 ,
but with only very mild monotonicity assumptions.
,
but with only very mild monotonicity assumptions.

