We study the uniqueness of positive solutions of the boundary-value problem
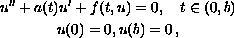
where
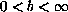 ,
,
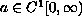 and
and
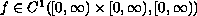 satisfy suitable
conditions. The proof of our main result is based on the shooting method
and the Sturm comparison theorem.
satisfy suitable
conditions. The proof of our main result is based on the shooting method
and the Sturm comparison theorem.
Yulian An, Ruyun Ma
Abstract:
We study the uniqueness of positive solutions of the boundary-value
problem
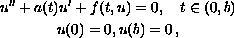
where
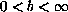 ,
,
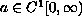 and
and
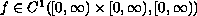 satisfy suitable
conditions. The proof of our main result is based on the shooting method
and the Sturm comparison theorem.
satisfy suitable
conditions. The proof of our main result is based on the shooting method
and the Sturm comparison theorem.
Submitted August 18, 2004. Published November 29, 2004.
Math Subject Classifications: 34B15.
Key Words: Boundary value problem; positive solutions; uniqueness;
shooting method; Sturm comparison theorem.
Show me the PDF file (153K), TEX file, and other files for this article.
 |
Yulian An School of Mathematics, Physics & Software Engineering Lanzhou Transportation University Lanzhou 730070, China email: yulian_an@tom.com |
|---|---|
 |
Ruyun Ma Department of Mathematics Northwest Normal University Lanzhou 730070, Gansu, China email: mary@nwnu.edu.cn |
Return to the EJDE web page