This paper addresses questions of existence and regularity of solutions to linear partial differential equations whose coefficients are generalized functions or generalized constants in the sense of Colombeau. We introduce various new notions of ellipticity and hypoellipticity, study their interrelation, and give a number of new examples and counterexamples. Using the concept of
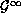 -regularity of generalized functions, we derive
a general global regularity result in the case of operators with
constant generalized coefficients, a more specialized result for
second order operators, and a microlocal regularity result for
certain first order operators with variable generalized coefficients.
We also prove a global solvability result for operators with constant
generalized coefficients and compactly supported Colombeau generalized
functions as right hand sides.
-regularity of generalized functions, we derive
a general global regularity result in the case of operators with
constant generalized coefficients, a more specialized result for
second order operators, and a microlocal regularity result for
certain first order operators with variable generalized coefficients.
We also prove a global solvability result for operators with constant
generalized coefficients and compactly supported Colombeau generalized
functions as right hand sides.

