We prove that the initial value problem associated with
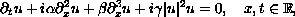
is locally well-posed in
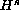 for
for
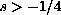 .
.
Xavier Carvajal
Abstract:
We prove that the initial value problem associated with
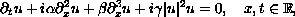
is locally well-posed in
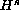 for
for
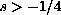 .
.
Submitted July 30, 2003. Published January 23, 2004.
Math Subject Classifications: 35Q58, 35Q60.
Key Words: Schrodinger equation, Korteweg-de Vries equation,
trilinear estimate, Bourgain spaces.
Show me the PDF file (230K), TEX file, and other files for this article.
 |
Xavier Carvajal IMECC-UNICAMP Caixa Postal: 6065 13083-859, Barao Geraldo Campinas, SP, Brazil email: carvajal@ime.unicamp.br |
|---|
Return to the EJDE web page