Electron. J. Diff. Eqns., Vol. 2004(2004), No. 10, pp. 1-20.
Trajectories connecting two submanifolds on a non-complete
Lorentzian manifold
Rossella Bartolo, Anna Germinario, & Miguel Sanchez
Abstract:
This article presents existence and multiplicity results for orthogonal
trajectories joining two submanifolds
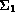 and
and
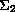 of a static space-time manifold
of a static space-time manifold
 under the action of gravitational
and electromagnetic vector potential. The main technical difficulties
are because
under the action of gravitational
and electromagnetic vector potential. The main technical difficulties
are because
 may not be complete and
may not be complete and
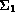 ,
,
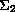 may not
be compact. Hence, a suitable convexity assumption and hypotheses
at infinity are needed. These assumptions are widely discussed in terms
of the electric and magnetic vector fields naturally associated.
Then, these vector fields become relevant from both their physical
interpretation and the mathematical gauge invariance of the equation
of the trajectories.
may not
be compact. Hence, a suitable convexity assumption and hypotheses
at infinity are needed. These assumptions are widely discussed in terms
of the electric and magnetic vector fields naturally associated.
Then, these vector fields become relevant from both their physical
interpretation and the mathematical gauge invariance of the equation
of the trajectories.
Submitted November 21, 2003. Published January 14, 2004.
Math Subject Classifications: 58E30, 53C50, 83C10, 83C50.
Key Words: Lorentzian manifolds, gravitational and electromagnetic fields,
convex boundary, critical point theory.
Show me the
PDF file (261K),
TEX file, and other files for this article.
 |
Rossella Bartolo
Dipartimento di Matematica
Politecnico di Bari
Via G. Amendola, 126/B
70126 Bari Italy
email: rossella@poliba.it
|
|---|
 |
Anna Germinario
Dipartimento di Matematica
Universita degli Studi di Bari
Via E. Orabona, 4
70125 Bari Italy
email: germinar@dm.uniba.it |
|---|
 |
Miguel Sanchez
Departamento de Geometria y Topologia
Fac. Ciencias, Univ. Granada
Avenida Fuentenueva s/n
18071 Granada Spain
email: sanchezm@ugr.es |
|---|
Return to the EJDE web page
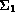 and
and
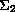 of a static space-time manifold
of a static space-time manifold
 under the action of gravitational
and electromagnetic vector potential. The main technical difficulties
are because
under the action of gravitational
and electromagnetic vector potential. The main technical difficulties
are because
 may not be complete and
may not be complete and
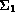 ,
,
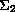 may not
be compact. Hence, a suitable convexity assumption and hypotheses
at infinity are needed. These assumptions are widely discussed in terms
of the electric and magnetic vector fields naturally associated.
Then, these vector fields become relevant from both their physical
interpretation and the mathematical gauge invariance of the equation
of the trajectories.
may not
be compact. Hence, a suitable convexity assumption and hypotheses
at infinity are needed. These assumptions are widely discussed in terms
of the electric and magnetic vector fields naturally associated.
Then, these vector fields become relevant from both their physical
interpretation and the mathematical gauge invariance of the equation
of the trajectories.


