We obtain sufficient conditions for the existence of at least three positive solutions for the equation
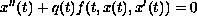
subject to some boundary conditions. This is an application of a new fixed-point theorem introduced by Avery and Peterson [6].
Zhanbing Bai, Yifu Wang, & Weigao Ge
Abstract:
We obtain sufficient conditions for the existence of
at least three positive solutions for the equation
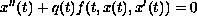
subject to some boundary conditions.
This is an application of a new fixed-point theorem
introduced by Avery and Peterson [6].
Submitted November 25, 2003. Published January 2, 2004.
Math Subject Classifications: 34B15.
Key Words: Triple positive solutions, boundary-value problem,
fixed-point theorem.
Show me the PDF file (184K), TEX file, and other files for this article.
 |
Zhanbing Bai Department of Applied Mathematics Beijing Institute of Technology, Beijing 100081, China Department of Applied Mathematics University of Petroleum, Dongying 257061, China email: baizhanbing@263.net |
|---|---|
| Yifu Wang Department of Applied Mathematics Beijing Institute of Technology, Beijing 100081, China email: yifu-wang@163.com | |
| Weigao Ge Department of Applied Mathematics Beijing Institute of Technology, Beijing 100081, China email: gew@bit.edu.cn |
Return to the EJDE web page