We obtain necessary and sufficient conditions for the integro-differential inequality
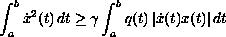
to be valid with one of the three boundary conditions:
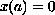 ,
or
,
or
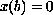 , or
, or
 .
For a power functions
.
For a power functions
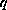 ,
the best constants
,
the best constants
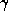 are found.
are found.
Evgeniy I. Bravyi & Sergey S. Gusarenko
Abstract:
We obtain necessary and sufficient conditions for the
integro-differential inequality
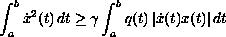
to be valid with one of the three boundary conditions:
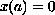 ,
or
,
or
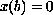 , or
, or
 .
For a power functions
.
For a power functions
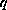 ,
the best constants
,
the best constants
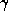 are found.
are found.
Submitted October 27, 2003. Published January 2, 2004.
Math Subject Classifications: 34K10, 34B30, 34B05, 41A44, 49J40, 58E35.
Key Words: Integral inequalities, integro-differential inequalities,
functional differential equations, variational problems.
Show me the PDF file (372K), TEX file, and other files for this article.
 |
Evgeniy I. Bravyi Research Centre "Functional Differential Equations" Perm State Technical University, Perm 614099, Russia email: bravyi@pi.ccl.ru |
|---|---|
 |
Sergey S. Gusarenko Department of Mathematical Analysis Perm State University, Perm 614099, Russia email: gusarenko@psu.ru |
Return to the EJDE web page