Electron. J. Diff. Eqns.,
Vol. 2003(2003), No. 97, pp. 1-14.
The heat equation and the shrinking
Masaki Kawagishi & Takesi Yamanaka
Abstract:
This article concerns the Cauchy problem for the partial
differential equation

Here
 and
and
 are real variables,
are real variables,
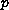 and
and
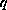 are positive
integers greater than 1, and the shrinking factors
are positive
integers greater than 1, and the shrinking factors
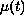 ,
,
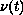 are positive-valued functions such that
their suprema are less than 1.
are positive-valued functions such that
their suprema are less than 1.
Submitted April 1, 2003. Published September 17, 2003.
Math Subject Classifications: 35K05, 35K55, 35R10, 49K25.
Key Words: Partial differential equation, heat equation,
shrinking, delay, Gevrey
Show me the
PDF file (229K),
TEX file, and other files for this article.
 |
Masaki Kawagishi
College of Science and Technology, Nihon University
Kanda-Surugadai, Chiyoda-ku, Tokyo 101-8308, Japan
email: masaki@suruga.ge.cst.nihon-u.ac.jp
|
|---|
 |
Takesi Yamanaka
College of Science and Technology, Nihon University
Kanda-Surugadai, Chiyoda-ku, Tokyo 101-8308, Japan
email: yamanaka@math.cst.nihon-u.ac.jp
|
|---|
Return to the EJDE web page

 and
and
 are real variables,
are real variables,
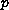 and
and
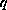 are positive
integers greater than 1, and the shrinking factors
are positive
integers greater than 1, and the shrinking factors
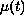 ,
,
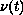 are positive-valued functions such that
their suprema are less than 1.
are positive-valued functions such that
their suprema are less than 1.

