Using both probabilistic and classical analytic techniques, we investigate the parabolic Kolmogorov equation
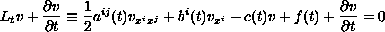
in
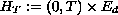 and its solutions when the coefficients are
bounded Borel measurable functions of
and its solutions when the coefficients are
bounded Borel measurable functions of
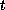 .
We show that the probabilistic
solution
.
We show that the probabilistic
solution
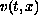 defined in
defined in
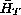 ,
is twice differentiable
with respect to
,
is twice differentiable
with respect to
 ,
continuously in
,
continuously in
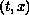 ,
once differentiable with respect to
,
once differentiable with respect to
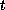 ,
a.e.
,
a.e.
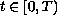 and satisfies the Kolmogorov equation
and satisfies the Kolmogorov equation
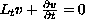 a.e. in
a.e. in
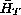 .
Our main tool
will be the Aleksandrov-Busemann-Feller Theorem. We also examine the
probabilistic solution to the fully nonlinear Bellman equation with
time-measurable coefficients in the simple case
.
Our main tool
will be the Aleksandrov-Busemann-Feller Theorem. We also examine the
probabilistic solution to the fully nonlinear Bellman equation with
time-measurable coefficients in the simple case
 .
We show that when the terminal data function is a paraboloid, the payoff
function has a particularly simple form.
.
We show that when the terminal data function is a paraboloid, the payoff
function has a particularly simple form.