Electron. J. Diff. Eqns., Vol. 2003(2003), No. 48, pp. 1-25.
Magnetic barriers of compact support and eigenvalues in
spectral gaps
Rainer Hempel & Alexander Besch
Abstract:
We consider Schr\"odinger operators
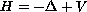 in
in
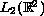 with a spectral gap, perturbed by a strong magnetic field
with a spectral gap, perturbed by a strong magnetic field
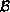 of compact support.
We assume here that the support of
of compact support.
We assume here that the support of
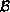 is connected and has
a connected complement; the total magnetic flux may be zero
or non-zero. For a fixed point
is connected and has
a connected complement; the total magnetic flux may be zero
or non-zero. For a fixed point
 in the gap, we show that
(for a sequence of couplings tending to
in the gap, we show that
(for a sequence of couplings tending to
 ) the signed
spectral flow across
) the signed
spectral flow across
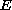 for the magnetic perturbation is equal
to the flow of eigenvalues produced by a high potential barrier
on the support of the magnetic field. This allows us to use
various estimates that are available for the high barrier case.
for the magnetic perturbation is equal
to the flow of eigenvalues produced by a high potential barrier
on the support of the magnetic field. This allows us to use
various estimates that are available for the high barrier case.
Submitted May 22, 2001. Published April 24, 2003.
Math Subject Classifications: 35J10, 81Q10, 35P20.
Key Words: Schrodinger operator, magnetic field, eigenvalues, spectral gaps,
strong coupling.
Show me the
PDF file (331K),
TEX file, and other files for this article.
 |
Rainer Hempel
Institut fur Analysis
Technische Universitat Braunschweig
Pockelsstrasse 14, 38106 Braunschweig
Germany
email: r.hempel@tu-bs.de |
|---|
 |
Alexander Besch
Institut fur Analysis
Technische Universitat Braunschweig
Pockelsstrasse 14, 38106 Braunschweig
Germany
Current address: Volkswagen AG, Wolfsburg, Germany
email: alexander.besch@volkswagen.de |
|---|
Return to the EJDE web page
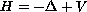 in
in
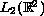 with a spectral gap, perturbed by a strong magnetic field
with a spectral gap, perturbed by a strong magnetic field
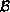 of compact support.
We assume here that the support of
of compact support.
We assume here that the support of
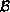 is connected and has
a connected complement; the total magnetic flux may be zero
or non-zero. For a fixed point
is connected and has
a connected complement; the total magnetic flux may be zero
or non-zero. For a fixed point
 in the gap, we show that
(for a sequence of couplings tending to
in the gap, we show that
(for a sequence of couplings tending to
 ) the signed
spectral flow across
) the signed
spectral flow across
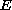 for the magnetic perturbation is equal
to the flow of eigenvalues produced by a high potential barrier
on the support of the magnetic field. This allows us to use
various estimates that are available for the high barrier case.
for the magnetic perturbation is equal
to the flow of eigenvalues produced by a high potential barrier
on the support of the magnetic field. This allows us to use
various estimates that are available for the high barrier case.

