We study the existence of weak solutions to the equation
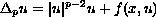
with the nonlinear boundary condition
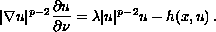
We assume Landesman-Lazer type conditions and use variational arguments to prove the existence of solutions.
Sandra Martinez & Julio D. Rossi
Abstract:
We study the existence of weak solutions to the equation
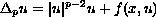
with the nonlinear boundary condition
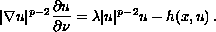
We assume Landesman-Lazer type conditions and use
variational arguments to prove the existence of solutions.
Submitted January 15, 2003. Published March 13, 2003.
Math Subject Classifications: 35P05, 35J60, 35J55.
Key Words: p-Laplacian, nonlinear boundary conditions, resonance.
Show me the PDF file (239K), TEX file, and other files for this article.
| Sandra Martinez Departamento de Matematica, FCEyN UBA (1428) Buenos Aires, Argentina email: smartin@dm.uba.ar | |
 |
Julio D. Rossi Departamento de Matematica, FCEyN UBA (1428) Buenos Aires, Argentina and Facultad de Matematicas, Universidad Catolica Casilla 306 Correo 22 Santiago, Chile email: jrossi@dm.uba.ar, jrossi@mat.puc.cl |
Return to the EJDE web page