Electron. J. Diff. Eqns., Vol. 2003(2003), No. 20, pp. 1-12.
Blow-up for p-Laplacian parabolic equations
Yuxiang Li & Chunhong Xie
Abstract:
In this article we give a complete picture of the blow-up criteria
for weak solutions of the Dirichlet problem
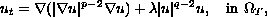
where
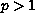 .
In particular, for
.
In particular, for
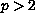 ,
,
 is the blow-up
critical exponent and we show that the sharp blow-up condition
involves the first eigenvalue of the problem
is the blow-up
critical exponent and we show that the sharp blow-up condition
involves the first eigenvalue of the problem

Submitted October 20, 2002. Published February 28, 2003.
Math Subject Classifications: 35K20, 35K55, 35K57, 35K65.
Key Words: p-Laplacian parabolic equations, blow-up,
global existence, first eigenvalue.
Show me the
PDF file (236K),
TEX file, and other files for this article.
 |
Yuxiang Li
Department of Mathematics
Nanjing University
Nanjing 210093, China
email: lieyuxiang@yahoo.com.cn |
|---|
 |
Chunhong Xie
Department of Mathematics
Nanjing University
Nanjing 210093, China |
|---|
Return to the EJDE web page
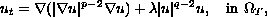
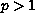 .
In particular, for
.
In particular, for
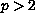 ,
,
 is the blow-up
critical exponent and we show that the sharp blow-up condition
involves the first eigenvalue of the problem
is the blow-up
critical exponent and we show that the sharp blow-up condition
involves the first eigenvalue of the problem


