Electron. J. Diff. Eqns., Vol. 2003(2003), No. 17, pp. 1-12.
Order and hyper-order of entire solutions of linear
differential equations with entire coefficients
Benharrat Belaidi & Karima Hamani
Abstract:
In this paper, we investigate the growth of solutions of
the differential equation
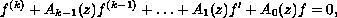
where
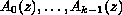 are entire functions with
are entire functions with
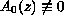 .
We will show that if the coefficients satisfy certain
growth conditions, then every finite order solution of the equation will
satisfy certain other growth conditions. We will also find conditions on the
coefficients so that every solution
.
We will show that if the coefficients satisfy certain
growth conditions, then every finite order solution of the equation will
satisfy certain other growth conditions. We will also find conditions on the
coefficients so that every solution
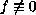 will have infinite order
and we estimate in one case the lower bounds of the hyper-order.
will have infinite order
and we estimate in one case the lower bounds of the hyper-order.
Submitted November 27, 2002. Published February 20, 2003.
Math Subject Classifications: 30D35, 34M10, 34C11.
Key Words: Linear differential equations, growth of entire functions,
hyper-order.
Show me the
PDF file (217K),
TEX file, and other files for this article.
 |
Benharrat Belaidi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem,
B. P 227 Mostaganem Algeria
e-mail: belaidi@univ-mosta.dz,
belaidi.benharrat@caramail.com |
|---|
 |
Karima Hamani
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem,
B. P 227 Mostaganem Algeria |
|---|
Return to the EJDE web page
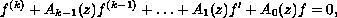
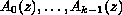 are entire functions with
are entire functions with
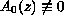 .
We will show that if the coefficients satisfy certain
growth conditions, then every finite order solution of the equation will
satisfy certain other growth conditions. We will also find conditions on the
coefficients so that every solution
.
We will show that if the coefficients satisfy certain
growth conditions, then every finite order solution of the equation will
satisfy certain other growth conditions. We will also find conditions on the
coefficients so that every solution
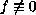 will have infinite order
and we estimate in one case the lower bounds of the hyper-order.
will have infinite order
and we estimate in one case the lower bounds of the hyper-order.

