Electron. J. Diff. Eqns., Vol. 2003(2003), No. 124, pp. 1-22.

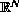
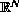
Resonance and strong resonance for semilinear elliptic equations in $\mathbb{R}^N$

Gabriel Lopez Garza & Adolfo J. Rumbos

Abstract:
We prove the existence of weak solutions for the semilinear elliptic problem
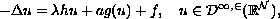
$$ -\Delta u=\lambda hu+ag(u)+f,\quad u\in \mathcal{D}^{1,2}({\mathbb{R}^N}), $$
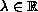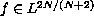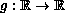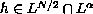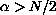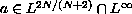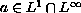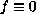where $\lambda \in \mathbb{R}$, $f\in L^{2N/(N+2)}$, $g:\mathbb{R} \to \mathbb{R}$ is a continuous bounded function, and $h \in L^{N/2}\cap L^{\alpha}$, $\alpha>N/2$. We assume that $a \in L^{2N/(N+2)}\cap L^{\infty}$ in the case of resonance and that $a \in L^1 \cap L^{\infty}$ and $f\equiv 0$ for the case of strong resonance. We prove first that the Palais-Smale condition holds for the functional associated with the semilinear problem using the concentration-compactness lemma of Lions. Then we prove the existence of weak solutions by applying the saddle point theorem of Rabinowitz for the cases of non-resonance and resonance, and a linking theorem of Silva in the case of strong resonance. 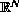The main theorems in this paper constitute an extension to $\mathbb{R}^N$ of previous results in bounded domains by Ahmad, Lazer, and Paul [2], for the case of resonance, and by Silva [15] in the strong resonance case.

Submitted June 3, 2003. Published December 16, 2003.
Math Subject Classifications: 35J20.
Key Words: Resonance, strong resonance, concentration-compactness.

Show me the PDF file (302K), TEX file, and other files for this article.

Gabriel Lopez Garza
Dept. of Math., Claremont Graduate University
Claremont California 91711, USA
email: Gabriel.Lopez@cgu.edu
Adolfo J. Rumbos
Department of Mathematics, Pomona College
Claremont, California 91711, USA
email: arumbos@pomona.edu

Return to the EJDE web page