We establish oscillation and nonoscilation criteria for the linear differential equation

where
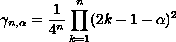
and
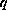 is a real-valued continuous function.
It is proved, using these criteria, that the equation
is a real-valued continuous function.
It is proved, using these criteria, that the equation
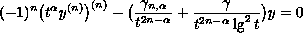
is nonoscillatory if and only if
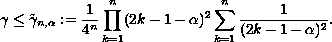
Ondrej Dosly & Simona Fisnarova
Abstract:
We establish oscillation and nonoscilation criteria for the linear
differential equation

where
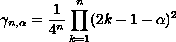
and
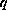 is a real-valued continuous function.
It is proved, using these criteria, that the equation
is a real-valued continuous function.
It is proved, using these criteria, that the equation
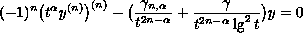
is nonoscillatory if and only if
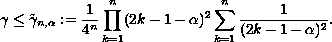
Submitted September 30, 2003. Published November 25, 2003.
Math Subject Classifications: 34C10
Key Words: Self-adjoint differential equation, variational method,
oscillation and nonoscillation criteria, conditional oscillation.
Show me the PDF file (274K), TEX file, and other files for this article.
 |
Ondrej Dosly Masaryk University, Janackovo nam. 2a CZ-662 95 Brno, Czech Republic email: dosly@math.muni.cz |
|---|---|
 |
Simona Fisnarova Masaryk University, Janackovo nam. 2a CZ-662 95 Brno, Czech Republic email: simona@math.muni.cz |
Return to the EJDE web page