Electron. J. Diff. Eqns., Vol. 2003(2003), No. 113, pp. 1-14.
Doubly nonlinear parabolic equations related to the
p-Laplacian operator: Semi-discretization
Fatiha Benzekri & Abderrahmane El Hachimi
Abstract:
We study the doubly nonlinear parabolic equation
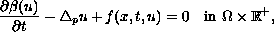
with Dirichlet boundary conditions and initial data.
We investigate a time-discretization of the continuous
problem by the Euler forward scheme. In addition to proving
existence, uniqueness and stability questions, we study the long
time behavior of the solution to the discrete problem.
We prove the existence of a global attractor, and obtain its
regularity under additional conditions.
Submitted April 16, 2003. Published November 11, 2003.
Math Subject Classifications: 35K15, 35K60, 35J60.
Key Words: P-Laplacian, nonlinear parabolic equations,
semi-discretization, discrete dynamical system, attractor.
Show me the
PDF file (240K),
TEX file, and other files for this article.
 |
Fatiha Benzekri
UFR Mathematiques Appliquees et Industrielles
Faculte des sciences
B. P. 20, El Jadida, Maroc
email: benzekri@ucd.ac.ma
|
|---|
 |
Abderrahmane El Hachimi
UFR Mathematiques Appliquees et Industrielles
Faculte des sciences
B. P. 20, El Jadida, Maroc
email: elhachimi@ucd.ac.ma
|
|---|
Return to the EJDE web page