Electron. J. Diff. Eqns., Vol. 2003(2003), No. 108, pp. 1-20.
Symmetry and monotonicity of solutions to some variational
problems in cylinders and annuli
Friedemann Brock
Abstract:
We prove symmetry and monotonicity properties for local minimizers
and stationary solutions of some variational problems
related to semilinear elliptic equations in a cylinder
 , where
, where
 is a bounded smooth domain in
is a bounded smooth domain in
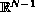 .
The admissible functions satisfy periodic boundary conditions on
.
The admissible functions satisfy periodic boundary conditions on
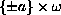 ,
and some other conditions.
We show also symmetry properties for related problems
in annular domains. Our proofs are based on rearrangement arguments
and on the Moving Plane Method.
,
and some other conditions.
We show also symmetry properties for related problems
in annular domains. Our proofs are based on rearrangement arguments
and on the Moving Plane Method.
Submitted March 9, 2003. Published October 24, 2003.
Math Subject Classifications: 35J25, 35B10, 35B35, 35B50, 35J20.
Key Words: Variational problem, periodic boundary conditions,
Neumann problem, symmetry of solutions, elliptic equation,
cylinder, annulus.
Show me the
PDF file (301K),
TEX file, and other files for this article.
Friedemann Brock
Universidad de Chile, Facultad de Ciencias
Departamento de Matematicas
Santiago de Chile, Casilla 653, Chile
email: fbrock@uchile.cl
Return to the EJDE web page
 , where
, where
 is a bounded smooth domain in
is a bounded smooth domain in
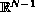 .
The admissible functions satisfy periodic boundary conditions on
.
The admissible functions satisfy periodic boundary conditions on
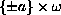 ,
and some other conditions.
We show also symmetry properties for related problems
in annular domains. Our proofs are based on rearrangement arguments
and on the Moving Plane Method.
,
and some other conditions.
We show also symmetry properties for related problems
in annular domains. Our proofs are based on rearrangement arguments
and on the Moving Plane Method.