 -regularity
result for generalized harmonic maps into spheres
-regularity
result for generalized harmonic maps into spheres
 -regularity
result for generalized harmonic maps into spheres
-regularity
result for generalized harmonic maps into spheres
Roger Moser
Abstract:
For
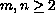 and
and
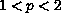 , we prove that a map
, we prove that a map
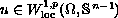 from an open domain
from an open domain
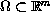 into the unit
into the unit
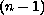 -sphere, which solves
a generalized version of the harmonic map equation,
is smooth, provided that
-sphere, which solves
a generalized version of the harmonic map equation,
is smooth, provided that
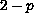 and
and
![$[u]_{{\rm BMO}(\Omega)}$](gifs/ah.gif) are both sufficiently
small.
This extends a result of Almeida [1].
The proof is based
on an inverse Holder inequality technique.
are both sufficiently
small.
This extends a result of Almeida [1].
The proof is based
on an inverse Holder inequality technique.
Submitted December 13, 2002. Published January 2, 2003.
Math Subject Classifications: 58E20.
Key Words: Generalized harmonic maps, regularity.
Show me the PDF file (247K), TEX file, and other files for this article.
 |
Roger Moser MPI for Mathematics in the Sciences Inselstr. 22-26, D-04103 Leipzig, Germany e-mail: moser@mis.mpg.de |
|---|
Return to the EJDE web page