Electron. J. Diff. Eqns., Vol. 2002(2002), No. 89, pp. 1-21.
Elliptic equations with one-sided critical growth
Marta Calanchi & Bernhard Ruf
Abstract:
We consider elliptic equations in bounded domains
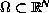 with
nonlinearities which have critical growth at
with
nonlinearities which have critical growth at
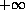 and linear growth
and linear growth
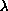 at
at
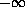 ,
with
,
with
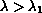 ,
the first eigenvalue of the Laplacian.
We prove that such equations have at least two solutions for
certain forcing terms provided
,
the first eigenvalue of the Laplacian.
We prove that such equations have at least two solutions for
certain forcing terms provided
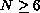 .
In dimensions
.
In dimensions
 an additional lower order growth term
has to be added to the nonlinearity, similarly as in the famous
result of Brezis-Nirenberg for equations with critical growth.
an additional lower order growth term
has to be added to the nonlinearity, similarly as in the famous
result of Brezis-Nirenberg for equations with critical growth.
Submitted March 01, 2002. Published October 18, 2002.
Math Subject Classifications: 35J20.
Key Words: Nonlinear elliptic equation, critical growth,
linking structure.
Show me the
PDF file (310K),
TEX file, and other files for this article.
 |
Marta Calanchi
Dip. di Matematica, Universita degli Studi,
Via Saldini 50, 20133 Milano, Italy
calanchi@mat.unimi.it, ph. +39.02.50316144 |
|---|
 |
Bernhard Ruf
Dip. di Matematica, Universita degli Studi,
Via Saldini 50, 20133 Milano, Italy
e-mail: ruf@mat.unimi.it, ph. +39.02.50316157 |
|---|
Return to the EJDE web page
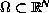 with
nonlinearities which have critical growth at
with
nonlinearities which have critical growth at
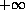 and linear growth
and linear growth
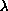 at
at
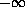 ,
with
,
with
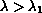 ,
the first eigenvalue of the Laplacian.
We prove that such equations have at least two solutions for
certain forcing terms provided
,
the first eigenvalue of the Laplacian.
We prove that such equations have at least two solutions for
certain forcing terms provided
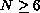 .
In dimensions
.
In dimensions
 an additional lower order growth term
has to be added to the nonlinearity, similarly as in the famous
result of Brezis-Nirenberg for equations with critical growth.
an additional lower order growth term
has to be added to the nonlinearity, similarly as in the famous
result of Brezis-Nirenberg for equations with critical growth.

