Electron. J. Diff. Eqns., Vol. 2002(2002), No. 86, pp. 1-6.
An embedding norm and the Lindqvist trigonometric functions
Christer Bennewitz & Yoshimi Saito
Abstract:
We shall calculate the operator norm
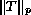 of the Hardy operator
of the Hardy operator
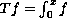 ,
where
,
where
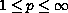 .
.
This operator is related to the Sobolev embedding operator from
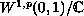 into
into
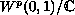 .
For
.
For
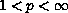 ,
the extremal, whose norm gives the operator norm
,
the extremal, whose norm gives the operator norm
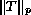 ,
is expressed in terms of the function
,
is expressed in terms of the function
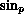 which is a generalization of the usual sine function and
was introduced by Lindqvist [6].
which is a generalization of the usual sine function and
was introduced by Lindqvist [6].
Submitted September 12, 2002. Published October 9, 2002.
Math Subject Classifications: 46E35, 33D05.
Key Words: Sobolev embedding operator, Volterra operator.
Show me the
PDF file (219K),
TEX file, and other files for this article.
Christer Bennewitz
Department of Mathematics, Lund University,
Box 118,22100 Sweden
e-mail: christer.bennewitz@math.lu.se
Yoshimi Saito
Dept. of Mathematics, University of Alabama at Birmingham,
Birmingham, AL 35294, USA.
e-mail: saito@math.uab.edu
Return to the EJDE web page
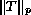 of the Hardy operator
of the Hardy operator 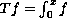 ,
where
,
where
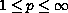 .
.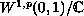 into
into
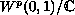 .
For
.
For
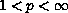 ,
the extremal, whose norm gives the operator norm
,
the extremal, whose norm gives the operator norm
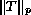 ,
is expressed in terms of the function
,
is expressed in terms of the function
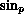 which is a generalization of the usual sine function and
was introduced by Lindqvist [6].
which is a generalization of the usual sine function and
was introduced by Lindqvist [6].