Electron. J. Diff. Eqns.,
Vol. 2002(2002), No. 76, pp. 1-12.
A viability result for second-order differential inclusions
Vasile Lupulescu
Abstract:
We prove a viability result for the second-order differential inclusion
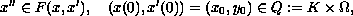
where
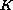 is a closed and
is a closed and
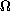 is an open subsets of
is an open subsets of
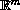 ,
and is an upper semicontinuous set-valued map with compact values,
such that
,
and is an upper semicontinuous set-valued map with compact values,
such that
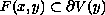 ,
for some convex proper lower semicontinuous function
,
for some convex proper lower semicontinuous function
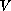 .
.
Submitted March 26, 2002. Published August 20, 2002
Math Subject Classifications: 34G20, 47H20.
Key Words: second-order contingent set, subdifferential, viable solution.
Show me the
PDF file (252K),
TEX file, and other files for this article.
 |
Vasile Lupulescu
Universitatea ``Constantin Brancusi'' of Targu-Jiu
Bulevardul Republicii, Nr.1
1400 T\^{a}rgu-Jiu, Romania
e-mail: vasile@utgjiu.ro |
|---|
Return to the EJDE web page
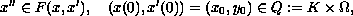
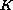 is a closed and
is a closed and
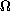 is an open subsets of
is an open subsets of
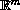 ,
and is an upper semicontinuous set-valued map with compact values,
such that
,
and is an upper semicontinuous set-valued map with compact values,
such that
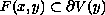 ,
for some convex proper lower semicontinuous function
,
for some convex proper lower semicontinuous function
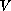 .
.
