A system of differential equations is permanent if there exists a fixed bounded set of positive states strictly bounded away from zero to which, from a time on, any positive initial data enter and remain. However, this fact does not happen for a differential equation with general non-autonomous terms. In this work we introduce the concept of pullback permanence, defined as the existence of a time dependent set of positive states to which all solutions enter and remain for suitable initial time. We show this behaviour in the non-autonomous logistic equation
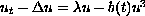 , with
, with
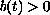 for all
for all
 ,
,
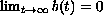 .
Moreover, a bifurcation scenario for the asymptotic behaviour of
the equation is described in a neighbourhood of the first eigenvalue
of the Laplacian. We claim that pullback permanence can be a suitable
tool for the study of the asymptotic dynamics for general
non-autonomous partial differential equations.
.
Moreover, a bifurcation scenario for the asymptotic behaviour of
the equation is described in a neighbourhood of the first eigenvalue
of the Laplacian. We claim that pullback permanence can be a suitable
tool for the study of the asymptotic dynamics for general
non-autonomous partial differential equations.

