Electron. J. Diff. Eqns., Vol. 2002(2002), No. 71, pp. 1-13.
Positive periodic solutions of functional
differential equations and population models
Daqing Jiang, Junjie Wei, & Bo Zhang
Abstract:
In this paper, we employ Krasnosel'skii's fixed point theorem
for cones to study the existence of positive periodic solutions
to a system of infinite delay equations,
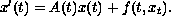
We prove two general theorems and establish new periodicity
conditions for several population growth models.
Submitted July 5, 2002. Published July 30, 2002.
Math Subject Classifications: 34K13, 92B05.
Key Words:
Functional differential equations, positive periodic
solution, population models.
Show me the
PDF file (251K),
TEX file, and other files for this article.
 |
Daqing Jiang
Department of Mathematics
Northeast Normal University
Changchun, Jilin 130024, China
e-mail: daqingjiang@vip.163.com |
|---|
 |
Junjie Wei
Department of Mathematics
Northeast Normal University
Changchun, Jilin 130024, China
e-mail: weijj@nenu.edu.cn |
|---|
 |
Bo Zhang
Department of Mathematics and Computer Science
Fayetteville State University
Fayetteville, NC 28301, USA
e-mail: bzhang@uncfsu.edu |
|---|
Return to the EJDE web page