Electron. J. Diff. Eqns., Vol. 2002(2002), No. 45, pp. 1-15.

Existence and regularity of a global attractor for doubly nonlinear parabolic equations

Abderrahmane El Hachimi & Hamid El Ouardi

Abstract:
In this paper we consider a doubly nonlinear parabolic partial differential equation
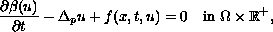
$$ \frac{\partial \beta (u)}{\partial t}-\Delta _{p}u+f(x,t,u)=0 \quad \hbox{in }\Omega \times\mathbb{R}^{+}, $$
with Dirichlet boundary condition and initial data given. We prove the existence of a global compact attractor by using a dynamical system approach. Under additional conditions on the nonlinearities 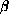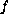$\beta$, $f$, and on 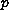$p$, we prove more regularity for the global attractor and obtain stabilization results for the solutions.

Submitted January 15, 2001. Published May 24, 2002.
Math Subject Classifications: 35K15, 35K60, 35K65.
Key Words: p-Laplacian, a-priori estimate, long time behaviour, dynamical system, absorbing set, global attractor.

Show me the PDF file (295K), TEX file, and other files for this article.

Abderrahmane El Hachimi
UFR Mathematiques Appliquees et Industrielles
Faculte des Sciences
B.P. 20, El Jadida - Maroc
e-mail: elhachimi@ucd.ac.ma
Hamid El Ouardi
Ecole Nationale Superieure d'Electricite et de Mecanique
B.P. 8118 -Casablanca-Oasis, Maroc
and
UFR Mathematiques Appliquees et Industrielles
Faculte des Sciences
B.P. 20, El Jadida - Maroc
e-mail: elouardi@ensem-uh2c.ac.ma

Return to the EJDE web page