Electron. J. Diff. Eqns., Vol. 2002(2002), No. 31, pp. 1-18.
Differential equations with several deviating arguments:
Sturmian comparison method in oscillation theory, II
Leonid Berezansky & Yury Domshlak
Abstract:
We study the oscillation of solutions to the differential
equation
![$$
\dot{x}(t) +a_1(t)x[r(t)]+a_2(t)x[p(t)]=0, \quad t\geq t_0
$$](gifs/aa.gif)
which has a retarded argument
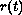 and an advanced argument
and an advanced argument
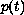 .
We obtain oscillation and non-oscillation conditions
which are closed to be necessary. We provide examples to show
that our results are best possible and compare them with
known results.
.
We obtain oscillation and non-oscillation conditions
which are closed to be necessary. We provide examples to show
that our results are best possible and compare them with
known results.
Submitted November 29, 2001. Published April 1, 2002.
Math Subject Classifications: 34K11.
Key Words: mixed differential equations, oscillation,
non-oscillation, Sturmian comparison method.
Show me the
PDF file (256K),
TEX file, and other files for this article.
 |
Leonid Berezansky
Department of Mathematics
Ben-Gurion University of the Negev
Beer-Sheva 84105, Israel
e-mail: brznsky@cs.bgu.ac.il |
|---|
 |
Yury Domshlak
Department of Mathematics
Ben-Gurion University of the Negev
Beer-Sheva 84105, Israel
e-mail: domshlak@cs.bgu.ac.il |
|---|
Return to the EJDE web page
![$$
\dot{x}(t) +a_1(t)x[r(t)]+a_2(t)x[p(t)]=0, \quad t\geq t_0
$$](gifs/aa.gif)
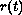 and an advanced argument
and an advanced argument
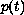 .
We obtain oscillation and non-oscillation conditions
which are closed to be necessary. We provide examples to show
that our results are best possible and compare them with
known results.
.
We obtain oscillation and non-oscillation conditions
which are closed to be necessary. We provide examples to show
that our results are best possible and compare them with
known results.

