Necessary and sufficient conditions are be given for the existence of analytic solutions of the nonhomogeneous n-th order differential equation at a singular point. Let
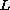 be a linear
differential operator with coefficients analytic at zero.
If
be a linear
differential operator with coefficients analytic at zero.
If
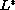 denotes the operator conjugate to
denotes the operator conjugate to
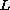 ,
then we will show
that the dimension of the kernel of
,
then we will show
that the dimension of the kernel of
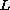 is equal to the dimension
of the kernel of
is equal to the dimension
of the kernel of
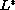 .
Certain representation theorems from
functional analysis will be used to describe the space of linear
functionals that contain the kernel of
.
Certain representation theorems from
functional analysis will be used to describe the space of linear
functionals that contain the kernel of
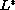 .
These results will
be used to derive a form of the Fredholm Alternative that will
establish a link between the solvability of
.
These results will
be used to derive a form of the Fredholm Alternative that will
establish a link between the solvability of
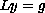 at a singular
point and the kernel of
at a singular
point and the kernel of
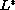 .
The relationship between the roots
of the indicial equation associated with
.
The relationship between the roots
of the indicial equation associated with
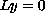 and the kernel of
and the kernel of
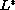 will allow us to show that the kernel of
will allow us to show that the kernel of
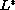 is spanned by a set of polynomials.
is spanned by a set of polynomials.
