Electron. J. Diff. Eqns., Vol. 2001(2001), No. 77, pp. 1-14.
Asymptotic behavior of solutions for some nonlinear
partial differential equations on unbounded domains
Jacqueline Fleckinger, Evans M. Harrell II, & Francois de Thelin
Abstract:
We study the asymptotic behavior of positive solutions
 of
of
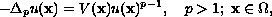
and related partial differential inequalities, as well
as conditions for existence of such solutions.
Here,
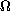 contains the exterior of a ball in
contains the exterior of a ball in
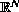
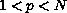 ,
,
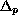 is the p-Laplacian, and
is the p-Laplacian, and
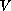 is a
nonnegative function. Our methods include generalized Riccati
transformations, comparison theorems, and the uncertainty
principle.
is a
nonnegative function. Our methods include generalized Riccati
transformations, comparison theorems, and the uncertainty
principle.
Submitted July 2, 2001. Published December 14, 2001.
Math Subject Classifications: 35B40, 35J60, 35J70.
Key Words: p-Laplacian, Riccati, uncertainty principle.
Show me the
PDF file (247K),
TEX file, and other files for this article.
An addendum was attached to this article on April 28, 2003.
See the last page of this article.
 |
Jacqueline Fleckinger
CEREMATH & UMR MIP, Universite Toulouse-1
21 allees de Brienne
31000 Toulouse, France
e-mail address: jfleck@univ-tlse1.fr |
 |
Evans M. Harrell II
School of Mathematics, Georgia Tech
Atlanta, GA 30332-0160, USA
e-mail address: harrell@math.gatech.edu
http://www.math.gatech.edu/~harrell/ |
 |
Francois de Thelin
UMR MIP, Universite Paul Sabatier
31062 Toulouse, France
e-mail address: dethelin@mip.ups-tlse.fr |
Return to the EJDE web page
 of
of
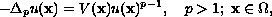
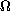 contains the exterior of a ball in
contains the exterior of a ball in
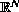
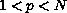 ,
,
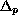 is the p-Laplacian, and
is the p-Laplacian, and
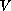 is a
nonnegative function. Our methods include generalized Riccati
transformations, comparison theorems, and the uncertainty
principle.
is a
nonnegative function. Our methods include generalized Riccati
transformations, comparison theorems, and the uncertainty
principle.


