Electron. J. Diff. Eqns., Vol. 2001(2001), No. 75, pp. 1-9.
A second order ODE with a nonlinear final condition
Pablo Amster & Maria Cristina Mariani
Abstract:
We study a semilinear second-order ordinary differential
equation with initial condition
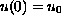 .
We prove the
existence of solutions satisfying a nonlinear final condition
.
We prove the
existence of solutions satisfying a nonlinear final condition
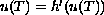 ,
under a certain growth condition.
Also we state conditions ensuring that any solution with
Cauchy data
,
under a certain growth condition.
Also we state conditions ensuring that any solution with
Cauchy data
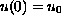 ,
,
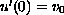 is defined on the whole interval
is defined on the whole interval
![$[0,T]$](gifs/ad.gif) .
.
Submitted October 15, 2000. Published December 10, 2001.
Math Subject Classifications: 34B15, 34C37.
Key Words: Nonlinear boundary-value problems, fixed point methods.
Show me the
PDF file (227K),
TEX file, and other files for this article.
 |
Pablo Amster
Departamento de Matematica,
Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires - CONICET,
Pab. I, Ciudad Universitaria,
(1428) Buenos Aires, Argentina
e-mail: pamster@dm.uba.ar |
|---|
 |
Maria Cristina Mariani
Departamento de Matematica,
Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires - CONICET,
Pab. I, Ciudad Universitaria,
(1428) Buenos Aires, Argentina
e-mail: mcmarian@dm.uba.ar |
|---|
Return to the EJDE web page
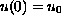 .
We prove the
existence of solutions satisfying a nonlinear final condition
.
We prove the
existence of solutions satisfying a nonlinear final condition
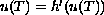 ,
under a certain growth condition.
Also we state conditions ensuring that any solution with
Cauchy data
,
under a certain growth condition.
Also we state conditions ensuring that any solution with
Cauchy data
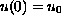 ,
,
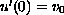 is defined on the whole interval
is defined on the whole interval
![$[0,T]$](gifs/ad.gif) .
.

