Electron. J. Diff. Eqns., Vol. 2001(2001), No. 74, pp. 1-10.
Sufficient conditions for functions to form Riesz bases
in L_2 and applications to nonlinear boundary-value problems
Peter E. Zhidkov
Abstract:
We find sufficient conditions for systems of functions to be
Riesz bases in
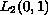 .
Then we improve a theorem
presented in [13] by showing that a ``standard'' system
of solutions of a nonlinear boundary-value problem, normalized
to 1, is a Riesz basis in
.
Then we improve a theorem
presented in [13] by showing that a ``standard'' system
of solutions of a nonlinear boundary-value problem, normalized
to 1, is a Riesz basis in
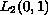 .
The proofs in this article use Bari's theorem.
.
The proofs in this article use Bari's theorem.
Submitted September 24, 2001. Published December 4, 2001
Math Subject Classifications: 41A58, 42C15, 34L10, 34L30.
Key Words: Riesz basis, infinite sequence of solutions,
nonlinear boundary-value problem.
Show me the
PDF file (240K),
TEX file, and other files for this article.
 |
Peter E. Zhidkov
Bogoliubov Laboratory of Theoretical Physics,
Joint Institute for Nuclear Research,
141980 Dubna (Moscow region), Russia
e-mail: zhidkov@thsun1.jinr.ru |
|---|
Return to the EJDE web page
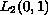 .
Then we improve a theorem
presented in [13] by showing that a ``standard'' system
of solutions of a nonlinear boundary-value problem, normalized
to 1, is a Riesz basis in
.
Then we improve a theorem
presented in [13] by showing that a ``standard'' system
of solutions of a nonlinear boundary-value problem, normalized
to 1, is a Riesz basis in
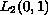 .
The proofs in this article use Bari's theorem.
.
The proofs in this article use Bari's theorem.
