Electron. J. Diff. Eqns., Vol. 2001(2001), No. 71, pp. 1-19.
Existence of solutions for quasilinear degenerate elliptic equations
Y. Akdim, E. Azroul, & A. Benkirane
Abstract:
In this paper, we study the existence of solutions for quasilinear
degenerate elliptic equations of the form
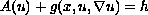 ,
where
,
where
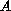 is a Leray-Lions operator from
is a Leray-Lions operator from
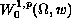 to its dual. On the nonlinear term
to its dual. On the nonlinear term
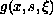 ,
we assume growth conditions on
,
we assume growth conditions on
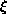 ,
not on
,
not on
 ,
and a sign condition on
,
and a sign condition on
 .
.
Submitted October 16, 2001. Published November 26, 2001.
Math Subject Classifications: 35J15, 35J20, 35J70.
Key Words: Weighted Sobolev spaces, Hardy inequality,
Quasilinear degenerate elliptic operators.
Show me the
PDF file (287K),
TEX file, and other files for this article.
 |
Y. Akdim
Departement de Mathematiques et Informatique,
Faculte des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fes, Maroc.
e-mail: y.akdim1@caramail.com |
|---|
 |
E. Azroul
Departement de Mathematiques et Informatique,
Faculte des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fes, Maroc.
e-mail: elazroul@caramail.com |
|---|
 |
A. Benkirane
Departement de Mathematiques et Informatique,
Faculte des Sciences Dhar-Mahraz,
B.P. 1796 Atlas, Fes, Maroc.
e-mail: abdelmoujib@iam.net.ma |
|---|
Return to the EJDE web page
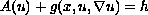 ,
where
,
where
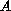 is a Leray-Lions operator from
is a Leray-Lions operator from
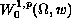 to its dual. On the nonlinear term
to its dual. On the nonlinear term
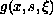 ,
we assume growth conditions on
,
we assume growth conditions on
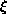 ,
not on
,
not on
 ,
and a sign condition on
,
and a sign condition on
 .
.


