Electron. J. Diff. Eqns., Vol. 2001(2001), No. 60, pp. 1-20.
Solutions of nonlinear parabolic equations without growth
restrictions on the data
Lucio Boccardo, Thierry Gallouet, & Juan Luis Vazquez
Abstract:
The purpose of this paper is to prove the existence of solutions
for certain types of nonlinear parabolic partial differential
equations posed in the whole space, when the data are assumed to
be merely locally integrable functions, without any control of
their behaviour at infinity. A simple representative example of
such an equation is

which admits a unique globally defined weak solution
 if
the initial function
if
the initial function
 is a locally integrable function in
is a locally integrable function in
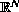 ,
,
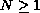 ,
and the second member
,
and the second member
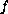 is a locally
integrable function of
is a locally
integrable function of
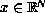 and
and
![$t\in [0,T]$](gifs/ah.gif) whenever
the exponent
whenever
the exponent
 is larger than 1.
The results extend to parabolic
equations results obtained by Brezis and by the authors for
elliptic equations. They have no equivalent for linear or sub-linear
zero-order nonlinearities.
is larger than 1.
The results extend to parabolic
equations results obtained by Brezis and by the authors for
elliptic equations. They have no equivalent for linear or sub-linear
zero-order nonlinearities.
Submitted July 17, 2001. Published September 12, 2001.
Math Subject Classifications: 35K55, 35K65.
Key Words: Nonlinear parabolic equations, global existence,
growth conditions.
Show me the
PDF file (413K),
TEX file, and other files for this article.
 |
Lucio Boccardo
Dipartimento di Matematica, Universita di Roma 1
Piazza A. Moro 2, 00185
Roma, Italy
e-mail: boccardo@mat.uniroma1.it |
|---|
 |
Thierry Gallouet
CMI, Universite de Marseille I
13453, France
e-mail: gallouet@cmi.univ-mrs.fr |
|---|
 |
Juan Luis Vazquez
Departamento de Matematicas
Universidad Autonoma de Madrid
28049 Madrid, Spain
e-mail: juanluis.vazquez@uam.es |
|---|
Return to the EJDE web page

 if
the initial function
if
the initial function
 is a locally integrable function in
is a locally integrable function in
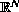 ,
,
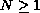 ,
and the second member
,
and the second member
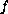 is a locally
integrable function of
is a locally
integrable function of
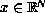 and
and
![$t\in [0,T]$](gifs/ah.gif) whenever
the exponent
whenever
the exponent
 is larger than 1.
The results extend to parabolic
equations results obtained by Brezis and by the authors for
elliptic equations. They have no equivalent for linear or sub-linear
zero-order nonlinearities.
is larger than 1.
The results extend to parabolic
equations results obtained by Brezis and by the authors for
elliptic equations. They have no equivalent for linear or sub-linear
zero-order nonlinearities.


