Electron. J. Diff. Eqns., Vol. 2001(2001), No. 48, pp. 1-19.
Global bifurcation result for the p-biharmonic operator
Pavel Drabek & Mitsuharu Otani
Abstract:
We prove that the nonlinear eigenvalue problem for the p-biharmonic
operator with
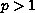 , and
, and
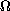 a bounded domain in
a bounded domain in
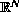 with smooth boundary, has principal positive eigenvalue
with smooth boundary, has principal positive eigenvalue
 which
is simple and isolated. The corresponding eigenfunction is positive in
which
is simple and isolated. The corresponding eigenfunction is positive in
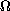 and satisfies
and satisfies
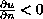 on
on
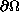 ,
,
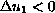 in
in
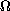 .
We also prove that
.
We also prove that
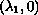 is the
point of global bifurcation for associated nonhomogeneous problem.
In the case
is the
point of global bifurcation for associated nonhomogeneous problem.
In the case
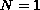 we give a description of all eigenvalues and
associated eigenfunctions. Every such an eigenvalue is then the point
of global bifurcation.
we give a description of all eigenvalues and
associated eigenfunctions. Every such an eigenvalue is then the point
of global bifurcation.
Submitted February 9, 2001. Published July 3, 2001.
Math Subject Classifications: 35P30, 34C23.
Key Words: p-biharmonic operator, principal eigenvalue, global bifurcation.
Show me the
PDF file (298K),
TEX file, and other files for this article.
 |
Pavel Drabek
Centre of Applied Mathematics
University of West Bohemia
Univerzitni 22, 306 14 Plzen
Czech Republic
e-mail: pdrabek@kma.zcu.cz |
|---|
 |
Mitsuharu Otani
Department of Applied Physics
School of Science and Engineering
Waseda University
3-4-1, Okubo Tokyo, Japan, 169-8555
e-mail: otani@mn.waseda.ac.jp |
|---|
Return to the EJDE web page
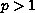 , and
, and
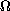 a bounded domain in
a bounded domain in
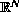 with smooth boundary, has principal positive eigenvalue
with smooth boundary, has principal positive eigenvalue
 which
is simple and isolated. The corresponding eigenfunction is positive in
which
is simple and isolated. The corresponding eigenfunction is positive in
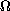 and satisfies
and satisfies
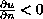 on
on
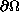 ,
,
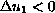 in
in
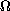 .
We also prove that
.
We also prove that
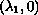 is the
point of global bifurcation for associated nonhomogeneous problem.
In the case
is the
point of global bifurcation for associated nonhomogeneous problem.
In the case
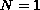 we give a description of all eigenvalues and
associated eigenfunctions. Every such an eigenvalue is then the point
of global bifurcation.
we give a description of all eigenvalues and
associated eigenfunctions. Every such an eigenvalue is then the point
of global bifurcation.

