Electron. J. Diff. Eqns., Vol. 2001(2001), No. 45, pp. 1-5.
A new proof for a Rolewicz's type theorem:
An evolution semigroup approach
C. Buse & S. S. Dragomir
Abstract:
Let
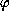 be a positive and non-decreasing function defined on the
real half-line and
be a positive and non-decreasing function defined on the
real half-line and
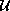 be a strongly continuous and
exponentially bounded evolution family of bounded linear operators
acting on a Banach space. We prove that if
be a strongly continuous and
exponentially bounded evolution family of bounded linear operators
acting on a Banach space. We prove that if
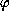 and
and
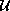 satisfy a certain integral condition (see the relation (2)
below) then
satisfy a certain integral condition (see the relation (2)
below) then
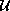 is uniformly exponentially stable. For
is uniformly exponentially stable. For
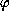 continuous, this result is due to S. Rolewicz.
continuous, this result is due to S. Rolewicz.
Submitted May 14, 2001. Published June 20, 2001.
Math Subject Classifications: 47A30, 93D05, 35B35, 35B40, 46A30.
Key Words: Evolution family of bounded linear operators,
evolution operator semigroup, Rolewicz's theorem.
Show me the
PDF file (215K),
TEX file, and other files for this article.
Return to the EJDE web page
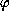 be a positive and non-decreasing function defined on the
real half-line and
be a positive and non-decreasing function defined on the
real half-line and
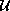 be a strongly continuous and
exponentially bounded evolution family of bounded linear operators
acting on a Banach space. We prove that if
be a strongly continuous and
exponentially bounded evolution family of bounded linear operators
acting on a Banach space. We prove that if
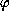 and
and
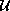 satisfy a certain integral condition (see the relation (2)
below) then
satisfy a certain integral condition (see the relation (2)
below) then
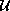 is uniformly exponentially stable. For
is uniformly exponentially stable. For
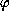 continuous, this result is due to S. Rolewicz.
continuous, this result is due to S. Rolewicz.

