We prove the existence of non-constant T-periodic orbits of the Hamiltonian system
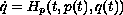
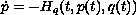 ,
,where H is a T-periodic function in t, non-convex and non-coercive in (p,q), and has the form
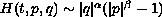 with
with
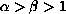 .
.
Morched Boughariou
Abstract:
We prove the existence of non-constant T-periodic
orbits of the Hamiltonian system
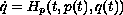
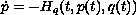 ,
,
where H is a T-periodic function in t,
non-convex and non-coercive in (p,q), and has the form
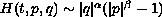 with
with
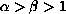 .
.
Submitted January 3, 2001. Published May 28, 2001.
Math Subject Classifications: 34C25, 37J45.
Key Words: Hamiltonian systems, non-coercive, periodic solutions, minimax argument.
Show me the PDF file (284K), TEX file, and other files for this article.
 |
Morched Boughariou Faculte des Sciences de Tunis Departement de Mathematiques, Campus Universitaire, 1060 Tunis, Tunisie e-mail: Morched.Boughariou@fst.rnu.tn |
|---|
Return to the EJDE web page