Electron. J. Diff. Eqns., Vol. 2001(2001), No. 36, pp. 1-9.
Multiplicity of forced oscillations for scalar differential equations
Massimo Furi, Maria Patrizia Pera, & Marco Spadini
Abstract:
We give, via topological methods, multiplicity results for small
periodic perturbations of scalar second order differential
equations. In particular, we show that the equation
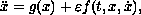
where
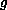 is
is
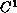 and
and
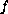 is continuous and periodic in
is continuous and periodic in
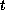 ,
has
,
has
 forced oscillations, provided that
forced oscillations, provided that
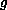 changes sign
changes sign
 times (
times (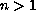 ).
).
Submitted December 31, 2000. Published May 21, 2001.
Math Subject Classifications: 34C25, 34C60.
Key Words: Forced oscillations, ordinary differential equations,
multiplicity of periodic solutions.
Show me the
PDF file (227K),
TEX file, and other files for this article.
 |
Massimo Furi
Dipartimento di Matematica Applicata ``G. Sansone''
Via S. Marta 3, 50139 Firenze, Italy
e-mail: furi@dma.unifi.it |
|---|
 |
Maria Patrizia Pera
Dipartimento di Matematica Applicata ``G. Sansone''
Via S. Marta 3, 50139 Firenze, Italy
e-mail: pera@dma.unifi.it |
|---|
 |
Marco Spadini
Dipartimento di Matematica Applicata ``G. Sansone''
Via S. Marta 3, 50139 Firenze, Italy
e-mail: spadini@dma.unifi.it |
|---|
Return to the EJDE web page
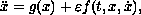
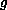 is
is
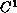 and
and
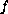 is continuous and periodic in
is continuous and periodic in
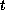 ,
has
,
has
 forced oscillations, provided that
forced oscillations, provided that
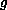 changes sign
changes sign
 times (
times (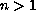 ).
).


