Electron. J. Diff. Eqns., Vol. 2001(2001), No. 32, pp. 1-19.
Cauchy problem for derivors in finite dimension
Jean-François Couchouron, Claude Dellacherie, & Michel Grandcolas
Abstract:
In this paper we study the uniqueness of solutions to
ordinary differential equations which fail to satisfy
both accretivity condition and the uniqueness condition of
Nagumo, Osgood and Kamke.
The evolution systems considered here are governed by a
continuous operators
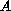 defined on
defined on
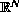 such that
such that
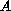 is a derivor; i.e.,
is a derivor; i.e.,
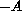 is quasi-monotone with respect to
is quasi-monotone with respect to
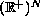 .
.
Submitted December 4, 2000. Published May 8, 2001.
Math Subject Classifications: 34A12, 34A40, 34A45, 34D05.
Key Words: derivor, quasimonotone operator, accretive operator,
Cauchy problem, uniqueness condition.
Show me the
PDF file (519K),
TEX file, and other files for this article.
 |
Jean-Francois Couchouron
UFR MIM Departement de Mathematiques
Universite de Metz
Ile du Saulcy
57045 Metz Cedex 01 France
e-mail: couchour@loria.fr |
|---|
|
Dellacherie Claude
Departement de Mathematiques
UFR Sciences, Site Colbert, Universite de Rouen
76821 Mont Saint Aignan, france
e-mail: dellache@univ-rouen.fr |
|---|
 |
Michel Grandcolas
UFR MIM Departement de Mathematiques
Universite de Metz
Ile du Saulcy
57045 Metz Cedex 01 France
e-mail: grandcol@poncelet.univ-metz.fr |
|---|
Return to the EJDE web page
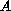 defined on
defined on
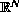 such that
such that
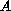 is a derivor; i.e.,
is a derivor; i.e.,
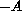 is quasi-monotone with respect to
is quasi-monotone with respect to
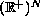 .
.

