The initial value problem for the Korteweg-deVries equation on the line is shown to be globally well-posed for rough data. In particular, we show global well-posedness for initial data in
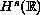 for -3/10 < s.
for -3/10 < s.
J. Colliander, M. Keel, G. Staffilani, H. Takaoka, & T. Tao
Abstract:
The initial value problem for the Korteweg-deVries equation
on the line is shown to be globally well-posed for rough data.
In particular, we show global well-posedness for
initial data in
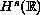 for -3/10 < s.
for -3/10 < s.
Submitted January 31, 2001. Published April 27, 2001.
Math Subject Classifications: 35Q53, 42B35, 37K10.
Key Words: Korteweg-de Vries equation, nonlinear dispersive equations,
bilinear estimates.
Show me the PDF file (236K), TEX file, and other files for this article.
| James Colliander Department of Mathematics, University of California Berkeley, California, 94720-3840 USA e-mail: colliand@math.berkeley.edu | |
 |
Markus Keel Department of Mathematics Caltech Pasadena, California, 91125, USA e-mail: keel@cco.caltech.edu |
 |
Gigliola Staffilani Department of Mathematics Stanford University Stanford, California, 94305, USA e-mail: gigliola@math.stanford.edu |
| Hideo Takaoka Division of Mathematics, Graduate School of Science Hokkaido University Sapporo, 060-0810, Japan. e-mail: takaoka@math.sci.hokudai.ac.jp | |
 |
Terence Tao Department of Mathematics University of California, Los Angeles, California, 90095-1596, USA e-mail: tao@math.ucla.edu |
Return to the EJDE web page