We survey recent results and present a number of open problems concerning the large-time behavior of solutions of semilinear parabolic equations with gradient nonlinearities. We focus on the model equation with a dissipative gradient term
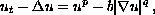
where
Philippe Souplet
Abstract:
We survey recent results and present a number of open problems
concerning the large-time behavior of solutions of semilinear parabolic
equations with gradient nonlinearities.
We focus on the model equation with a dissipative gradient term
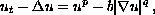
where
Submitted February 19, 2001. Published March 26, 2001.
Math Subject Classifications: 35K55, 35B35, 35B40, 35B33, 35J60.
Key Words: nonlinear parabolic equations, gradient term,
finite time blowup, global existence.
Show me the PDF file (284K), TEX file, and other files for this article.
 |
Philippe Souplet Departement de Mathematiques, Universite de Picardie INSSET, 02109 St-Quentin, France and Laboratoire de Mathematiques Appliquees UMR CNRS 7641, Universite de Versailles 45 avenue des Etats-Unis, 78035 Versailles, France. e-mail: souplet@math.uvsq.fr |
|---|
Return to the EJDE web page