Electron. J. Diff. Eqns., Vol. 2001(2001), No. 17, pp. 1-19.
Homogenization of a nonlinear degenerate parabolic differential equation
A. K. Nandakumaran & M. Rajesh
Abstract:
In this article, we study the homogenization of the nonlinear
degenerate parabolic equation
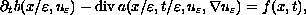
with mixed boundary conditions(Neumann and Dirichlet)
and obtain the limit equation as
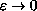 .
We also prove corrector results to improve the weak convergence of
.
We also prove corrector results to improve the weak convergence of
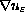 to strong convergence.
to strong convergence.
Submitted September 11, 2000. Published March 15, 2001.
Math Subject Classifications: 35B27, 74Q10.
Key Words: degenerate parabolic equation, homogenization,
two-scale convergence, correctors.
Show me the
PDF file (292K),
TEX file, and other files for this article.
 |
A. K. Nandakumaran
Department of Mathematics
Indian Institute of Science
Bangalore- 560 012, India
e-mail: nands@math.iisc.ernet.in |
|---|
 |
M. Rajesh
Department of Mathematics
Indian Institute of Science
Bangalore- 560 012, India
e-mail: rajesh@math.iisc.ernet.in |
|---|
Return to the EJDE web page
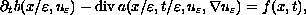
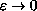 .
We also prove corrector results to improve the weak convergence of
.
We also prove corrector results to improve the weak convergence of
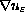 to strong convergence.
to strong convergence. 
